- 最大流
- 最小费用最大流
最大流
引入
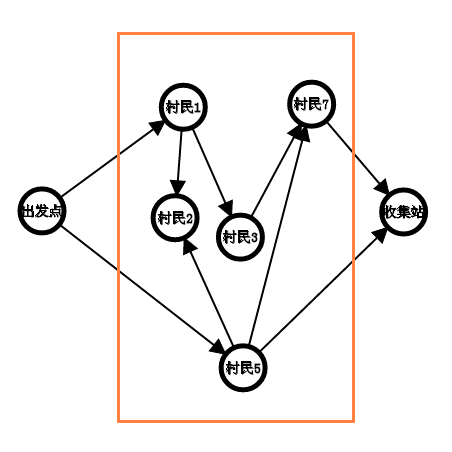
假设你所在的村庄开通了地下流水管道,自来水厂源源不断的提供水,村民们用水直接或间接用水,而村庄用完的废水统一回收于另一点(设从自来水厂流出的水全部回收)。当然每个管道有一定的容量,求出废水站最多可以汇聚多少水。
概念
**容量:**每条边都有一个容量(水管的最大水流容量) **源点:**出发点(水厂) **汇点:**结束点(废水站) **流:**一个合法解称作一个流,也就是一条可以从源点到汇点的一条合法路径。 **流量:**每条边各自被经过的次数称作其流量,最终收集的总数为整个流的流量。
限制
**容量限制:**每条边的流量不超过其容量(水管会爆炸) **流量平衡:**对于除源点和汇点以外的点来说,其流入量一定等于流出量。
解决
现在我们简化一下这个图,来解决这个问题。
x/y表示总流量为y,已经流了x
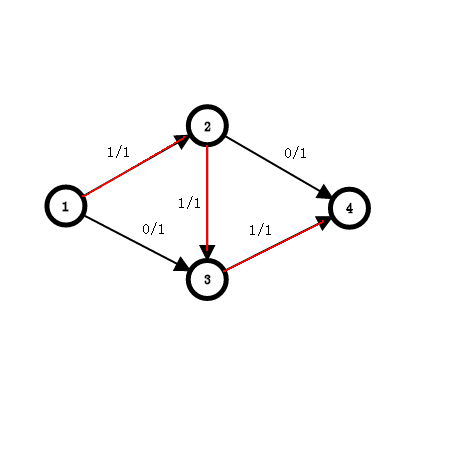
首先我们会想到找随即路径,然而如果走到如上图所示。
当走完 1->2->3->4 我们就找不到其他路径了,那么答案为1吗?不,答案为2.
那么现在我们改进算法,给流过的路径建立反向边
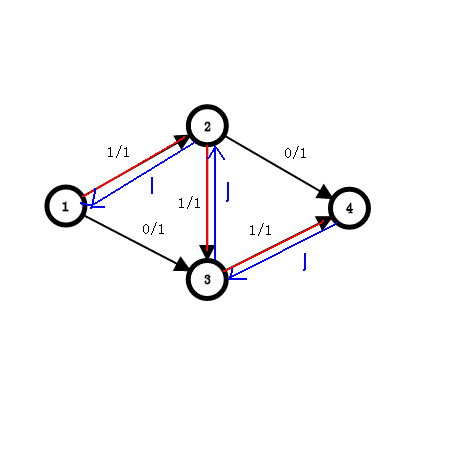
这样就给了一个反悔的机会。
定义一跳变得残量为:容量-已流过的流量
反向边的流量值=正向流过的总流量,也就是说正向流过多少,反向就可以流回多少。
从而我们又找到 1->3->2->4 的一条路径
再次建路径上的反向边,我们发现没有路径可以到达4点,所以答案为2.
小结
- 在图上找到一条从源点到汇点的路径(称为“增广路”)
- 去增广路上的残量最小值v(也就是流过的路径中流量最小的那一个)
- 将答案加上v
- 将增广路上所有边的残量减去v,反向边的残量加上v
重复上边四个步骤直到找不到增广路为止,这称作 FF 方法
首先这个算法必定不会死循环,因为每次增广都会导致流量增加(并且增加的是整数),而且流量有一个客观存在的最大值,所以它必定结束。
由于我们并没有指定它走那一条边,所以优先考虑随便走一条边。
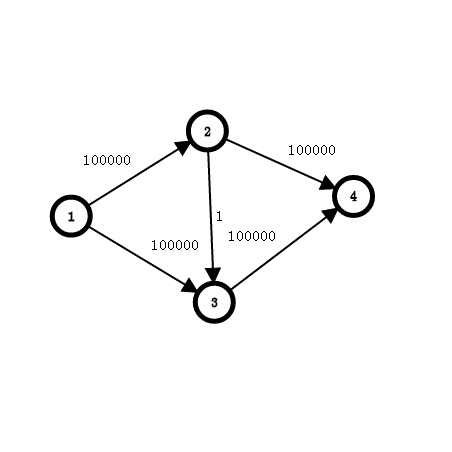
考虑一种极限的情况:
现增广 1->2->3->4 会出现一条 3->2 容量为1的边。
再增广 1->3->2->4 ,再增广 1->2->3->4 …
浪费大量的时间,如果脸黑的话最多2e5次
然而我们如果先 1->2->4 然后 1->3->4 走两次就好了。
上面的做法是我们不期望的。我们可以考虑每次增广最短路 (EK算法)
EK算法
EK算法是以上算法的实现:每次寻找最短路进行增广。
时间复杂度 $_math_inline$O(m^2n)$math_inline_$
结构体储存三个变量 next to dis 【邻接表建边】
flow[i]:表示流过i点的v值,也就是说目前经过到i点的路径上的最小的残量。
dis[i]:表示i点距离源点的距离,S,T表示源点以及汇点
首先我们利用bfs处理图的连通性以及所有点于源点的距离,当然,当这条边上的残量已经为0的时候,我们认为它已经不能经过,我们可以直接不考虑。
在bfs中国呢pre数组是记录每个点最短路的前驱,last数组记录上条边的编号,从而记录出最短路径,然后从汇点进行更新即可。
Code
1bool bfs(int s,int t) {
2 memset(flow,0x7f,sizeof(flow));
3 memset(dis,0x7f,sizeof(dis));
4 memset(vis,0,sizeof(vis));
5 Q.push(s);vis[s]=1;dis[s]=0,pre[t]=-1;
6
7 while(!Q.empty()) {
8 int temp=Q.front();
9 Q.pop();
10 vis[temp]=0;
11 for(int i=head[temp];i!=-1;i=edge[i].nxt) {
12 int v=edge[i].to;
13
14 if(edge[i].flow>0&&dis[v]>dis[temp]+edge[i].dis) {
15 dis[v]=dis[temp]+edge[i].dis;
16 pre[v]=temp;
17 last[v]=i;
18 flow[v]=min(flow[temp],edge[i].flow);
19 if(!vis[v]) {
20 vis[v]=1;
21 Q.push(v);
22 }
23 }
24 }
25 }
26 return pre[t]!=-1;
27}
从汇点向前更新
Code
1while(bfs(s,t)) {
2 int now=t;
3 maxflow+=flow[t];
4 mincost+=flow[t]*dis[t];
5 while(now!=s) {
6 edge[last[now]].flow-=flow[t];
7 edge[last[now]^1].flow+=flow[t];
8 now=pre[now];
9 }
10 }
最大流最小割定理
什么是割?
比如:你的仇人是一个工厂老板。你要炸掉一些车,让他每个货物都运不到销售点。炸掉越大的车,你越容易被发现。你希望炸掉的车的容量之和尽量小,最小化这个值
选出一些边的集合,使得删除他们之后从源点无法到达汇点,那么这个集合就叫做一个割。这些边的容量之和叫做这个割的容量
**定理1:**任取一个割,其容量大于最大流的流量
从源点汇点每次都会经过割上的最少一条边。
割掉这条边以后,把源点能到达的边放在左边,不能到达的放在右边。
显然源点到汇点的流量不会超过从左边走向右边的次数,而这又不会超过从左边到右边的容量之和
**直观一点:**假设你是在车装着货物的时候炸掉了它。
每个货物你至少付出1的代价炸掉(流量小于容量的时候你要付出比货物数更多的代价),所以你炸的代价不会小于货物数
定理2: 最小割的容量大于最大流的流量,且FF方法能够正确的求出它。
这意味着一个惊人的事实:你能够仅付出和货物数相同的代价,就把你的仇人的财路炸断
考虑FF算法结束时,残量网络上没有了增广路
那么我们假设这个时候,从源点经过残量网络能达到的点组成的集合为X,不能达到的点为Y。显然汇点在Y例,并且残量网络上没有从X到Y的边。
可以发现以下事实成立:
- Y到X的边流量为0,如果流量不为0,那么应该存在一条从X到Y的反向边,于是矛盾
- X到Y的边流量等于其容量。只有这样它才不会在残量网络中出现
根据第一个条件,我们可以得知:没有流量从过年X到Y之后又回到X,所以当前流量应该等于X到Y的边的流量之和,根据第二个条件它又等于从X到Y的边容量之和,而所有从X到Y的边又构成一个割,其容量等于这些边的容量之和。
这意味着我们找到一个流和一个割,使得前者的流量等于后者的容量。
而根据前面的结论,最大流的流量不会超过这个割的容量,所以这个流一定是最大流。
荣养的,最小割的容量也不会小于这个流的流量,所以这个割也一定是最小割。
这就是FF法最后的局面(由于FF会终止,所以它必定求出这样一个局面),由此我们得出:FF是正确的,并且最大流等于最小割
EK优化-Dinic
EK时间复杂度太高,虽然大多数情况跑不到上界。
有一个显然的优化:
如果增广一次后发现最短路没有变化,那么可以继续增广,直到源点到汇点的增广路增大,才需要一遍bfs。
bfs之后我们除去那些可能在最短路上的边,即dis[终点]=dis[起点]+1的那些边
显然这些边构成的图中没有环,我们只需要沿这些边尽可能的增广即可
Code
1int bfs() {
2 memset(dis,-1,sizeof(dis));
3 dis[S]=0;
4 Q.push(S);
5 while(!Q.empty()) {
6 int u=Q.front();
7 Q.pop() ;
8 for(int i=head[u];i!=-1;i=edge[i].nxt) {
9 int v=edge[i].to;
10 if(dis[v]==-1&&edge[i].w>0) {
11 dis[v]=dis[u]+1; //更新
12 Q.push(v);
13 }
14 }
15 }
16 return dis[T]!=-1; //判断是否联通。
17}
当图连通时进行dfs,当前节点为u,每次经过与u距离最近的点,并且这条边的残量值要大于0,然后往后进行dfs。
我们在dfs时要加一个变量,作为流量控制(最后的流量不能超过前边流量的最小值)
dfs中变量flow记录这条管道之后的最大流量
Code
1bool dfs(int u,int exp) {
2 if(u==T)return exp; //到达重点,全部接受。
3 int flow=0,tmp=0;
4 for(int i=head[u];i!=-1;i=edge[i].nxt) {
5 int v=edge[i].to; //下一个点。
6 if(dis[v]==dis[u]+1&&edge[i].w>0) {
7 tmp=dfs(v,min(exp,edge[i].w)); //往下进行
8 if(!tmp)continue;
9
10 exp-=tmp; //流量限制-流量,后边有判断。
11 flow+=tmp;
12
13 edge[i].w-=tmp; //路径上的边残量减少
14 edge[i^1].w+=tmp; //流经的边的反向边残量增加。
15 if(!exp)break; //判断是否在限制边缘
16 }
17 }
18 return flow;
19}
重复上边如果图连通(有最短路径),就一直增广
while(bfs())ans+=dfs(S,inf);
时间复杂度 $_math_inline$O(n^2m)$math_inline_$
在某些特殊情况下(每个点要么只有一条入边且容量为1,要么仅有一条出边且容量为1)其时间复杂度甚至能做到 $_math_inline$O(m\sqrt(n))$math_inline_$
Template
最大流模版 - 链式前向星存图
1struct Flow_Dinic {
2 Flow_Dinic(int n) {
3 head = vector<int>(n + 10, -1);
4 level = vector<int>(n + 10);
5 }
6
7 struct edge {
8 int to, cap, next;
9 };
10
11 vector<int> head;
12 vector<int> level;
13
14 int s = 0, t = 0; // max_flow from s to t
15
16 vector<struct edge> edge;
17
18 void add_edge(int u, int v, int c) {
19 edge.push_back((struct edge) {v, c, head[u]});
20 head[u] = edge.size() - 1;
21 edge.push_back((struct edge) {u, 0, head[v]});
22 head[v] = edge.size() - 1;
23 }
24
25 bool bfs() {
26 fill(level.begin(), level.end(), 0);
27 level[s] = 1;
28 queue<int> que;
29 que.push(s);
30 while (!que.empty()) {
31 for (int i = head[que.front()]; ~i; i = edge[i].next) {
32 if (edge[i].cap && !level[edge[i].to]) {
33 level[edge[i].to] = level[que.front()] + 1;
34 que.push(edge[i].to);
35 if (edge[i].to == t) return true;
36 }
37 }
38 que.pop();
39 }
40 return false;
41 }
42
43 int dfs(int f, int u) {
44 if (u == t) return f;
45 int d = 0, used = 0;
46 for (int i = head[u]; ~i; i = edge[i].next) {
47 if (edge[i].cap && level[u] == level[edge[i].to] - 1) {
48 if ((d = dfs(min(f - used, edge[i].cap), edge[i].to))) {
49 edge[i].cap -= d;
50 edge[i ^ 1].cap += d;
51 used += d;
52 }
53 }
54 }
55 if (!used) level[u] = 0;
56 return used;
57 }
58
59 long long run(int _s, int _t) {
60 s = _s;
61 t = _t;
62 long long max_flow = 0;
63 while (bfs()) {
64 int d = 0;
65 while ((d = dfs(0x3f3f3f3f, s))) max_flow += d;
66 }
67 return max_flow;
68 }
69 };
最大流模版 - FAST - 邻接表存图
1 struct Dinic {
2 Dinic(int n) {
3 G = vector<vector<int> >(n + 10);
4 d = vector<int> (n+10);
5 vis = vector<bool> (n+10);
6 cur = vector<int> (n+10);
7 }
8
9 struct Edge {
10 int from, to, cap, flow;
11 };
12
13 int s, t; //节点数,边数,源点编号,汇点编号
14 vector<Edge> edges; //边表,edges[e]和edges[e^1]互为反向弧
15 vector<vector<int> > G; //邻接表,G[i][j]表示节点i的第j条边在e中的序号
16 vector<bool> vis; //bfs用
17 vector<int> d; //从起点到i的距离
18 vector<int> cur; //当前弧下标
19 void add_edge(int from, int to, int cap) {
20 edges.push_back({from, to, cap, 0});
21 edges.push_back({to, from, 0, 0});
22 G[from].push_back(edges.size() - 2);
23 G[to].push_back(edges.size() - 1);
24 }
25
26 bool BFS() {
27 fill(vis.begin(), vis.end(), false);
28 queue<int> q;
29 q.push(s);
30 d[s] = 0;
31 vis[s] = true;
32 while (!q.empty()) {
33 for (int id : G[q.front()]) {
34 Edge &e = edges[id];
35 if (!vis[e.to] && e.cap > e.flow) {
36 vis[e.to] = true;
37 d[e.to] = d[q.front()] + 1;
38 q.push(e.to);
39 }
40 }
41 q.pop();
42 }
43 return vis[t];
44 }
45
46 long long DFS(int u, int a) {
47 if (u == t || a == 0) return a;
48 int flow = 0, f;
49 for (int &i = cur[u]; i < (int) G[u].size(); ++i) {
50 Edge &e = edges[G[u][i]];
51 if (d[u] + 1 == d[e.to] &&
52 (f = DFS(e.to, min(a, e.cap - e.flow))) > 0) {
53 e.flow += f;
54 edges[G[u][i] ^ 1].flow -= f;
55 flow += f;
56 a -= f;
57 if (a == 0) break;
58 }
59 }
60 return flow;
61 }
62
63 long long run(int _s, int _t) {
64 s = _s;
65 t = _t;
66 long long flow = 0;
67 while (BFS()) {
68 fill(cur.begin(), cur.end(), 0);
69 flow += DFS(s, 0x3f3f3f3f);
70 }
71 return flow;
72 }
73 };
最小费用最大流
除另有声明外,本博客文章均采用 知识共享 (Creative Commons) 署名 4.0 国际许可协议 进行许可。转载请注明原作者与文章出处。