| path | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 3 | 2 | 3 | ∞ | ∞ | ∞ | ∞ |
| 2 | 3 | 0 | ∞ | ∞ | 5 | 4 | ∞ | ∞ |
| 3 | 2 | ∞ | 0 | ∞ | ∞ | 4 | 6 | ∞ |
| 4 | 3 | ∞ | ∞ | 0 | 4 | ∞ | 6 | ∞ |
| 5 | ∞ | 5 | ∞ | 4 | 0 | 2 | 2 | ∞ |
| 6 | ∞ | 4 | 4 | ∞ | 2 | 0 | ∞ | 3 |
| 7 | ∞ | ∞ | 6 | 6 | 2 | ∞ | 0 | 3 |
| 8 | ∞ | ∞ | ∞ | ∞ | ∞ | 3 | 3 | 0 |
| dis | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 估计值 | 0 | 3 | 2 | 3 | ∞ | ∞ | ∞ | ∞ |
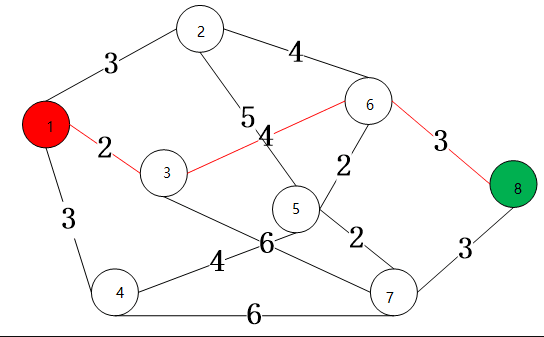
path代表地图 例如path[i][j]代表从i到j的距离
dis代表从起点到达i的距离,开始时初始化为最大,代表无穷远即未连同
vis代表当前节点[i]是否访问过
既然是求 1 号顶点到其余各个顶点的最短路程,那就先找一个离 1 号顶点最近的顶点。通过数组 dis 可知当前离 1 号顶点最近是 3 号顶点。
当选择了 3 号顶点后,dis[3]的值就已经从“估计值”变为了“确定值”,即 1 号顶点到 3 号顶点的最短路程就是当前 dis[3]值。因为目前离 1 号顶点最近的是 3 号顶点,并且这个图所有的边都是正数,那么肯定不可能通过第三个顶点中转,使得 1 号顶点到 3 号顶点的路程进一步缩短了。因为 1 号顶点到其它顶点的路程肯定没有 1 号到 3 号顶点短。
既然选了 3 号顶点,接下来再来看 3 号顶点有哪些出边呢。有 3->6 和 3->7 这两条边。先讨论通过 3->6 这条边是否能够让 1 号顶点到 6 号顶点的路程变短。也就是说比较dis[6]和dis[3]+path[3][6]的大小。其中 dis[3] 表示 1 号顶带你到 3 号顶点的路程。dis[3]+path[3][6]中dis[3]表示 1 号顶点到 3 号顶点的路程,path[3][6]表示 3->6 这条边。所以 dis[3]+path[3][6]就表示从1号顶带你到3号顶点,再通过3->6这条边到达3号顶点的路程
我们发现 dis[6]=∞,dis[3]+path[3][6]=6,dis[6] > dis[3]+path[3][6],因此dis[6]要更新为10。这个过程有个专业术语叫“松弛”。即 1 号顶点到 3 号顶点的路程即 dis[3] ,通过 3->6 这条边松弛成功。这便是Dijkstra算法的主要思想:通过“边”来松弛 1 号顶点到其余各个顶点的路程。
算法的基本思想是:每次找到离源点(上面例子的源点就是 1 号顶点)最近的一个顶点,然后以该顶点为中心进行扩展,最终得到源点到其余所有点的最短路径。基本步骤如下:
- 将所有的顶点分为两部分:已知最短路程的顶点集合 P 和未知最短路径的顶点集合 Q。最开始,已知最短路径的顶点集合 P 中只有源点一个顶点。我们这里用一个
vis[ i ]数组来记录哪些点在集合 P 中。例如对于某个顶点 i,如果vis[ i ]为 1 则表示这个顶点在集合 P 中,如果vis[ i ]为 0 则表示这个顶点在集合 Q 中。 - 设置源点 s 到自己的最短路径为 0 即 dis=0。若存在源点有能直接到达的顶点 i,则把
dis[ i ]设为path[s][ i ]。同时把所有其它(源点不能直接到达的)顶点的最短路径为设为 ∞。 - 在集合 Q 的所有顶点中选择一个离源点 s 最近的顶点 u(即
dis[u]最小)加入到集合 P。并考察所有以点 u 为起点的边,对每一条边进行松弛操作。例如存在一条从 u 到 v 的边,那么可以通过将边 u->v 添加到尾部来拓展一条从 s 到 v 的路径,这条路径的长度是dis[u]+path[u][v]。如果这个值比目前已知的dis[v]的值要小,我们可以用新值来替代当前dis[v]中的值。 - 重复第 3 步,如果集合 Q 为空,算法结束。最终 dis 数组中的值就是源点到所有顶点的最短路径。
in
18 13
21 2 3
31 3 2
41 4 3
52 6 4
62 5 5
73 6 4
83 7 6
94 5 4
104 7 6
116 8 3
126 5 2
135 7 2
147 8 3
out
11 to 2 min= 3
21 to 3 min= 2
31 to 4 min= 3
41 to 5 min= 7
51 to 6 min= 6
61 to 7 min= 8
71 to 8 min= 9
1#include <iostream>
2#include <string.h>
3#include <cstdio>
4#include <stdlib.h>
5#include <limits.h>
6
7
8using namespace std;
9const int INF = 0x3f3f3f3f;
10#define maxn 1000+100
11int path[maxn][maxn], dis[maxn]; // 地图 起点到达i的距离
12bool vis[maxn]; // 是否访问过
13int n, t; // 地标数 路径数
14
15void init() {
16 for (int i = 0; i < maxn; ++i) {
17 for (int j = 0; j < maxn; ++j) {
18 path[i][j] = INF;
19 }
20 path[i][i] = 0;
21 }
22}
23
24void dijkstra(){
25 // 将1到i的距离初始化
26 for (int i = 1; i <= n; i++) {
27 dis[i] = path[1][i];
28 vis[i] = false;
29 }
30 vis[1] = true; // 标记起点为访问过的
31 dis[1] = 0; // 起点到起点的距离为0
32 for (int i = 2; i <= n; i++) { // 从2号节点遍历到n号节点
33 int now = -1, minL = INF;
34 // 遍历一遍dis数组,寻找到未访问过的到1最短的路径长度
35 for (int j = 1; j <= n; j++) { // 从1到n
36 if (!vis[j] && minL > dis[j]) { // 如果没有访问过当前节点,并且当前从1到j的距离小于最大长度
37 now = j; // 更新最短路径的位置
38 minL = dis[j]; // 最短距离等于当前
39 }
40 }
41 if (now == -1) break; // 未找到
42 vis[now] = true; // 将now标记为访问过
43 // 从1开始寻找到j最短的路径
44 for (int j = 1; j <= n; j++) {
45 // 没有访问过 并且当前已走的长度加上走到j节点的长度小于当前dis[j]
46 if (!vis[j] && (dis[now] + path[now][j]) < dis[j]) {
47 dis[j] = dis[now] + path[now][j]; // 更新从起点到j的最短路径
48 }
49 }
50 }
51}
52
53int main() {
54 freopen("in.txt", "r", stdin); // 从指定文件输入数据 提交时注释掉
55// memset(path, INT_MAX, sizeof(path));
56 while (scanf("%d %d", &n, &t) != EOF) {
57 init();
58 for (int i = 0; i < t; i++) {
59 int from, to, len;
60 scanf("%d %d %d", &from, &to, &len);
61 if (path[from][to] > len)
62 path[from][to] = path[to][from] = len;
63 }
64 dijkstra();
65 for (int i = 1; i <= n; i++) {
66 printf("1 to %d min= %d\n", i, dis[i]);
67 }
68 }
69 return 0;
70}
除另有声明外,本博客文章均采用 知识共享 (Creative Commons) 署名 4.0 国际许可协议 进行许可。转载请注明原作者与文章出处。